contact@triforce.fyi
April 10, 2024 [last updated 5.27.24]
C. Brian Conkle
Vancouver, WA
Gravity is hardly the whole story here. It’s barely a footnote, though it is a place to start.
Down toward the bottom, I provide evidence that protons are spinors. So, stay tuned for the Coded Prime Set (or click here.)
Once you understand the Coded Prime Set, you are ready for the real lesson; the Mechanical Prime Set. Click here.
*** 5.27.24 update *** I adjusted some of the language to hammer home the interrelationship of uncertainty and isotropy.
Science is an incredibly useful tool, but it has limits. One limitation is the requirement that the frame of reference utilized is always that of the observer, situated in spacetime. Any activity that places the frame of reference anywhere but with the observer, by definition, is not scientific.
As it happens, the only way to understand gravity in harmony with all other observed forces described by the Standard Model of Particle Physics is to place the frame of reference within the particle itself, rather than the spacetime observer. In simplest terms, you must be the particle (insert Caddyshack 2 .gif here) and nothing else. Critically, reassigning the frame of reference to the particle eliminates the confusion caused by isotropy which permits everything else to just fall into place.
Within the particle itself, space and time have no general meaning. Within the particle, what matters is:
1. the isotropic frame of reference;
2. the certainty and uncertainty of position and momentum;
3. internal degrees of freedom, including the manner of expression at different numbers of degrees of freedom, ranging from zero to four;
4. magnetic moment; and
5. anomalous magnetic moment.
There are 5 fundamental scales, each corresponding to the number of internal degrees of freedom of a particle (call them dimensions if you must; I don’t want to but I think I need to):
(0) Singularity “Planck” Scale (below 10 to the -35m);
(1) Vector “Mycelial” Scale (between 10 to the -35m and 10 to the -20m);
(2) Quantum Scale (between 10 to the -20m and 10 to the -9m);
(3) Classical “Life” Scale (between 10 to the -9m and 10 to the 25m, or thereabouts); and
(4) Cosmic Scale (above 10 to the 25m, or thereabouts).
Internal degrees of freedom share an inverse relationship with isotropy. At the Singularity Scale, isotropy is essentially unrestricted (and yes, 0-dimensional physics is a thing.) At the Vector Scale, isotropy is restricted one-dimensionally, at the Quantum Scale 2-dimensionally, 3-dimensonally at the Classical Scale and 4-dimensionally at the Cosmic Scale. Think about it this way. If something exists 2-dimensionally, how can it have a fixed reference point in 3 dimensions? The simple answer is that it cannot, hence the isotropy. In essence, isotropy is the universe’s version of a “null” value; akin to what is known (but generally disfavored) in the realm of computer programming. Eitherwise, it needs to be understood that an “internal degree of freedom” is also a “degree of isotropic restriction.”
Cracking on… gravity arises at the Vector (Mycelial) Scale. It is an expression of vectored (i.e., expressed along a single “one-dimensional” internal degree of freedom) electron magnetic moment. This is why, among other things, gravity always points back toward the electron (and why positrons generate anti-gravity.) In simplest terms, relative to our own frame of reference; gravity is how electrons behave when expressing along one “real” (i.e., “kinetic,” used interchangeably hereafter) dimension and two isotropic dimensions.
An electron’s magnetic moment is anti-parallel to spin, so when spin is expressed one-dimensionally as a vector, the magnetic moment likewise expresses as a vector, pointing in the opposite direction of momentum; this means back toward the particle as opposed to out from it (subject to the slight offset of the electron’s small anomalous magnetic moment.)
Gravity being vector-mechanical in nature rather than quantum-mechanical is also why it appears so much weaker than quantum electromagnetism, the weak force and the strong force. Each of the latter three forces express quantum mechanically (i.e., two kinetic dimensions and one isotropic, relative to us) whereas gravity is vector-mechanical (i.e., one kinetic dimension and two isotropic, relative to us) electromagnetism.
The upshot here is that mass/energy increase exponentially with the increased number of degrees of freedom along which a particle expresses. In other words, expressing along kinetic dimensions increases mass/energy while expressing isotropically does not. The mass/energy increase from combining multiple kinetic dimensions is exponential (i.e., a logarithmic increase) rather than additive.
This begs reexamining the answers to some basic questions. What are mass and energy, why do they exist and why they are not conserved quantities? Or, perhaps the question is how are they conserved quantities? I suppose it depends on whether you are a glass half-full or glass half-empty sort of person.
It is well understood that mass and energy are equivalent. That’s the whole point of special relativity. What needs to be understood now is that mass and energy are themselves expressions of a particle’s positional certainty which directly corresponds to its momentum uncertainty. The greater a particle’s positional certainty (i.e. the lower its momentum certainty or the greater its momentum uncertainty) the greater its mass and energy.
Also, and this is critical:
isotropic = potential
The mass/energy of a particle is determined by the certainty/uncertainty (isotropy) of its momentum and position. It is well understood and uncontroversial that energy can be either kinetic or potential. Likewise, momentum and position (and thereby mass) can be either kinetic or potential.
Certain momentum is potential, while uncertain (isotropic) momentum is kinetic (because things can hit you from any direction.) Conversely, certain position is kinetic (because you can hit things in any direction) while uncertain (isotropic) position is potential.
At the Singularity “Planck” Scale, momentum is essentially zero. Zero is the most certain number. Ergo, at the Singularity Scale, momentum is essentially, completely certain (I note “essentially” because the cosmos tends not to permit absolutes… it insists we take everything with a grain of salt.) Position at this scale is therefore essentially, completely uncertain. Both momentum and position at the Singularity Scale are essentially completely isotropic. This means that essentially nothing can interact with the particle, at any time or from any direction or distance.
Conversely to zero, infinity is the least certain number. At the Cosmic Scale, therefore, where particles express along four internal degrees of freedom (i.e., 4-dimensionally;) momentum is essentially completely uncertain while position is essentially completely certain. In other words, both momentum and position have shed all isotropy and are essentially completely kinetic. This means anything any everything can interact with the particle, at any and all times, from any and all directions and distances.
In between these two extremes, we have the Vector (Mycelial), Quantum and Classical Scales wherein we see momentum and position certainty and uncertainty switch places one internal degree of freedom at a time.
Human consciousness is primarily bound up in, and perceived solely as, the Classical Scale. This means we perceive 3 real dimensions and one isotropic. So, for example, when we look at quantum mechanical behaviors, we are perceiving two real dimensions and one isotropic. When we look at gravity we are perceiving it as one real dimension and two isotropic.
Similarly, when we look out at the stars (i.e., toward the Cosmic Scale,) we perceive the universe as isotropic. Astronomers tell us that the universe appears to extend out about evenly in all directions, as if the Earth were somehow the center of the universe. This is because, at the Classical Scale, we only have three real dimensions to work with; causing the fourth dimension to appear to us as isotropic.
Since mass and energy are expressions of a particle’s positional certainty, and momentum uncertainty increases with the number of internal degrees of freedom along which a particle is expressing; the higher the number of internal degrees of freedom, the higher the mass and energy.
Gravity is weaker than the other forces because gravity is electromagnetism expressed at one degree of freedom (i.e., one kinetic dimension and three isotropic (two from our perspective)) when the other forces express quantum-mechanically, along two internal degrees of freedom (i.e., two kinetic dimensions and two isotropic (one from our perspective.)) Keep in mind that all particles exist at all scales simultaneously, even if they have no, or virtually no, observable or intuitable expression at some scales.
This interpretation of particle physics is also consistent with why mass/energy is not conserved during neutron decay. When a neutron decays, it decays (typically) into a w-boson, which has 1,000 times more mass/energy than the neutron. The w-boson then decays into a proton, electron and anti-neutrino, all of which combined have about 1.5 electron masses less mass/energy than the neutron.
In short, the w-boson is the momentary spike in a neutron’s momentum uncertainty as it undergoes its transformation to its decay products, all of which combined have higher momentum certainty (therefore higher isotropy, lower positional certainty and less mass/energy) than the original neutron. Yes, the “Higgs boson” is a total scam… it’s like Blade said, “some [people are] always trying to ice-skate uphill.”
Here is a whiteboard I marked up for some additional context. Not all of it is relevant, some are interim notes, some parts are likely wrong… but most of it should be useful. The equations at the top correlate uncertainty (isotropy) with mass/energy.
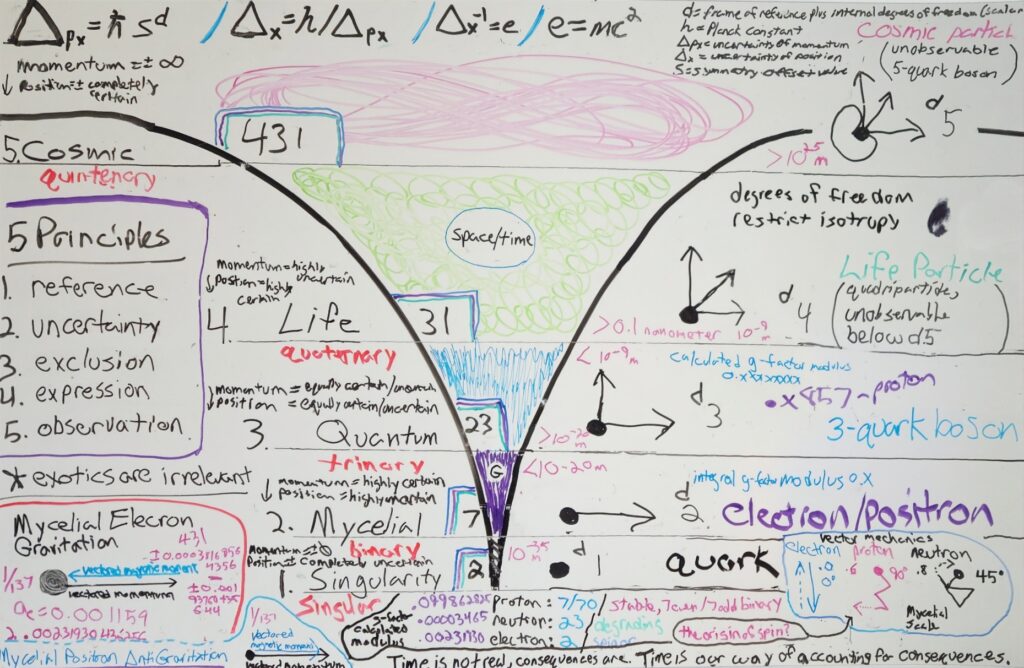
I labeled the second scale (1 degree of freedom) the “Mycelial” scale rather than the “Vector” scale in the above illustration in hopes it would help people visualize the behavior of vectored momentum, which is not too dissimilar to the way that fungi extend mycelial filaments to create underground networks. Gravitational waves can be particularly useful in understanding and visualizing the one-dimensional, mycelium-like behavior of particles.
We know that when a neutron decays, it essentially converts to a proton by throwing off an electron. Both the electron and proton would be new particles which would need to extend their vectored momentum, their mycelium, however far out they go among the mycelium of all the other electrons, protons and neutrons. This would not happen instantaneously because of limits like the speed of light. The best number I saw for the speed at which a gravitational wave propagates is about 0.1% the speed of light. Were an event to occur which resulted in a very large number of new electrons being generated in a concentrated area very quickly, the propagation of electron mycelium from that event would travel out as a gravitational wave as all those new electrons establish their places in the larger mycelial network.
I won’t go into it much here, but the use of a frame of reference without what we call spacetime requires a reinterpretation of what we call a “field.” Space does not exist and the universe has no intrinsic “field(s).” Rather, it is more like particles generate their own fields as a function of their degree of unrestricted isotropy which decreases as internal degrees of freedom increase.
In other words, when the movement of a particle along one or more dimensions is restricted by its scale; the particle takes on a “null” value for those dimensions as opposed to as zero value. The “null” value, much like in computer programming is a value that stands in for all possible outcomes, but does not express any individual outcome unless forced. The gravitational field of an electron (or positron) arises from these null values, which cause the particle to be sufficiently, spatially undefined so as to occupy an enormous amount (if not effectively all of) of what we perceive as space and/or the universe.
The trade-off is that, at the scale the electron (or positron) expresses gravity (or anti-gravity,) while it may somewhat slowly extend itself throughout the universe; it can only interact with the rest of the universe along a single kinetic dimension, and only weakly because the mass/energy of a particle, and therefore the influence of its magnetic moment, decreases logarithmically with the decrease in kinetic dimensions along which a particle expresses (corresponding to an increase in isotropic dimensions.)
In short, gravitational fields arise at the Mycelial (Vector) Scale (one real dimension, three isotropic.) They take the form of a large, interconnected mycelial network, driven by fermions (electrons and positrons,) but influencing (mostly) protons, anti-protons and neutrons, all of which have their own, more localized mycelium (see, the illustration in the bottom right corner of the whiteboard above.)
More generally speaking, I think it is fair to say that subject to the limitations of the (Pauli) Exclusion Principle, what we perceive as a field (i.e., space) is the extent to which each particle occupies the universe or a significant fraction thereof… sort of like a big bang universe, but without the bang. In short, the interplay between a particle’s intrinsic “field(s)” and the intrinsic “field(s)” of other particles is governed principally by both the Uncertainty Principle and (Pauli) Exclusion Principle, and as generally described by known physical laws. Ultimately, visualize and characterize in whatever way works for you, if it actually works for you; these are deep waters.
Same topic, different angle. Why hasn’t anyone ever looked at the additive modulo (2-dimensional rotation) for the calculated g-factors of the electron, proton and neutron? Here is one view of what that looks like with the positron and anti-proton thrown in for good measure:
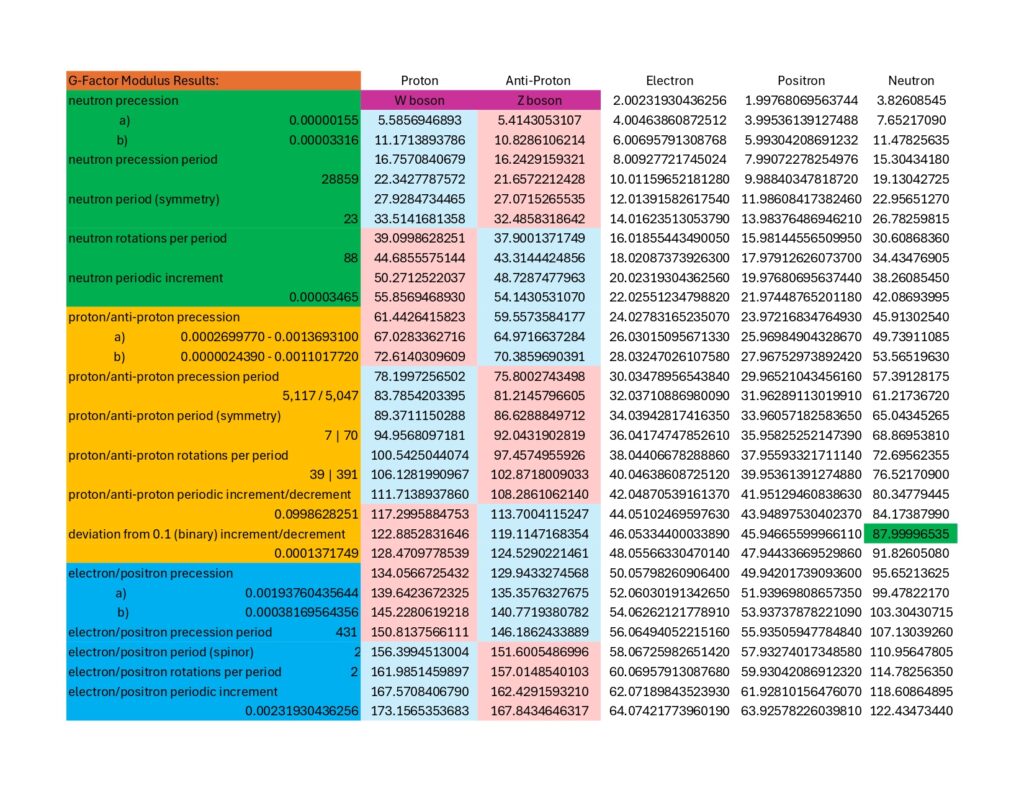
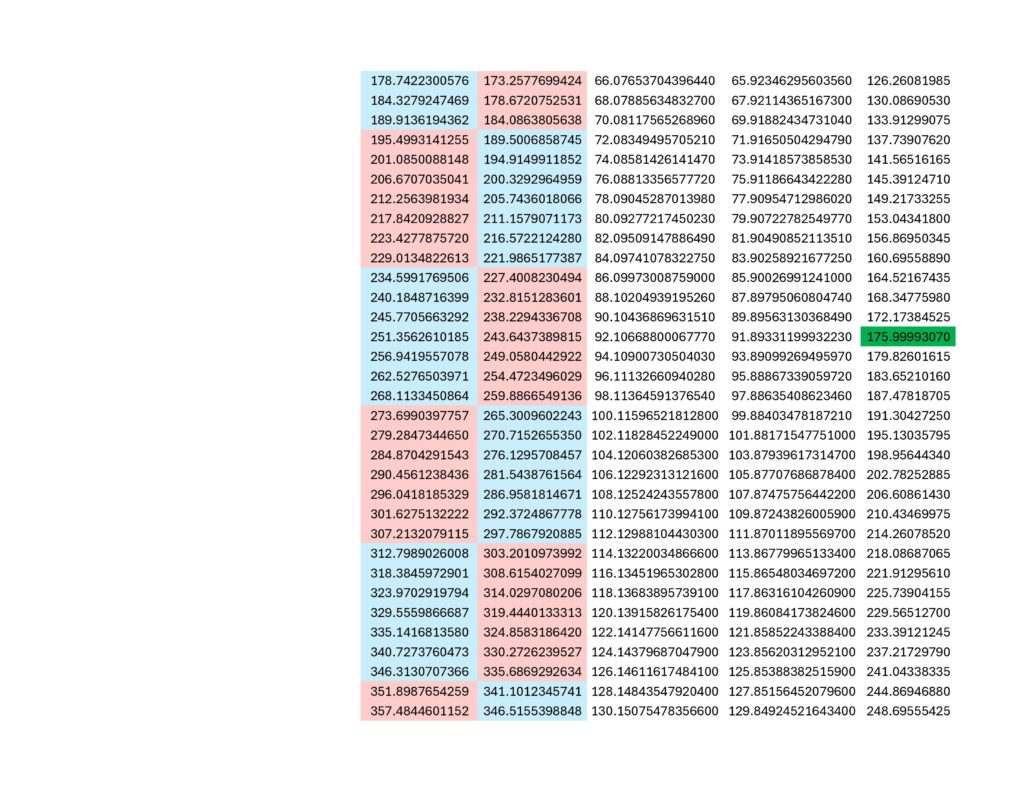
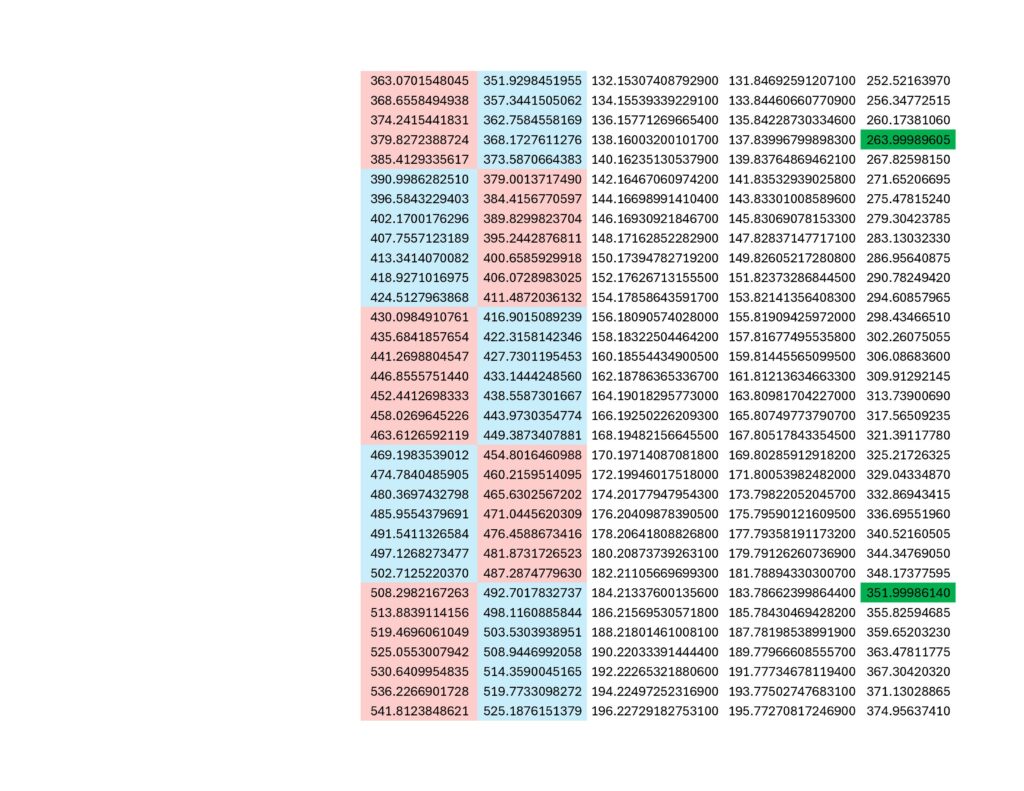
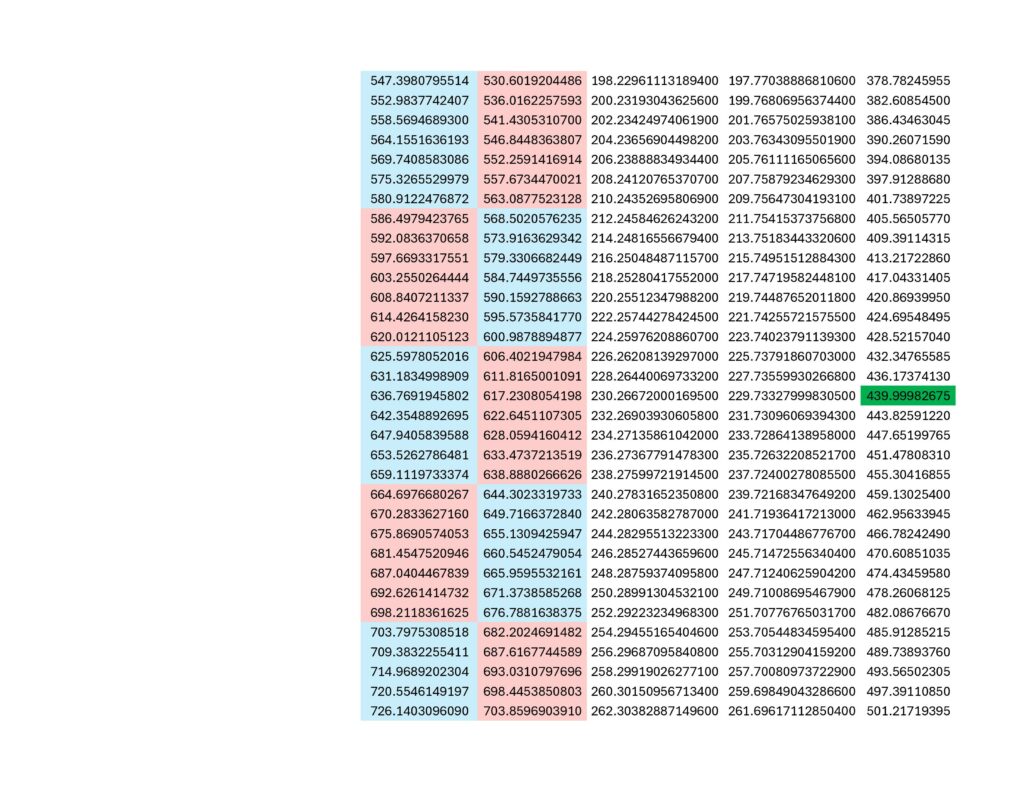
What does the above show? Lots. Among other things, it demonstrates that quantum mechanics is literally the observation of 2-dimensional behaviors of particles within the 3-diminsional observer frame of reference required by science. I know this is only a modicum of evidence, but that’s what the pages for the Coded Prime Set and Mechanical Prime Set are for. Isotropy is inherently confusing, so tread lightly.
Do you see the proton behaving as a spinor? That’s why I color-coded blue and red. The integral modulo or 1st-digit modulo (i.e., the first number to the right of the decimal point) repeats 7 odd numbers followed by 7 even numbers. Draw a sine wave around a circle numbered like a clock from 0 to 9 with the wave passing through the radius of each number once, in order, alternating between peaks and valleys for each number, and what you get is all the peaks on odd numbers and all the valleys on even numbers, or vice-versa. You can picture it like a 5-tooth gear or 5-pointed star if you want. Proton magnetic moment visits peaks 7 times in a row and then must visit valleys 7 times in a row before returning to peaks 7 times in a row and then valleys 7 times in a row, and so on and so forth.
There is room, right at the beginning, for the w-boson because the first odd set includes only 6 numbers, not 7. While that is not a unique occurrence in the modulo, it is rare; on the order of about one in five thousand. The 2nd-digit modulo (i.e., the second number to the right of the decimal point) controls where within the set of 7 the anomaly will occur as well as whether or not the symmetry will eventually break. The 2nd-digit modulo for the proton has a descending order (beginning with 9, 8, 7, 5, 4, 2, 1,) and since the proton has a descending periodic increment; the anomaly will always be corrected for at the end of a set. So, only sets of 6 and 7 are possible with sets of 7 being about five thousand times more likely than a set of 6. That relationship continues on into infinity (i.e., it remains stable and never breaks) and would present in something like a supercollider as an occasional spike in the mass/energy detected in a collision event. Eitherwise, it looks to me like protons are spinors, just like electrons… the other stable, charge-carrying particle. If you’re curious, the proton g-factor is 5.5856946893(16) (you can ignore the integer value, only the remainder is relevant.) This places it (more or less) within the .X857142 subgroup of the .857142 7-fold prime symmetry. Here is a visual (note that only X=1, X=3 and X=5 behave as spinors, with X=5 incrementing 0.1 while X=1 increments 0.3 and X=3 increments 0.7):
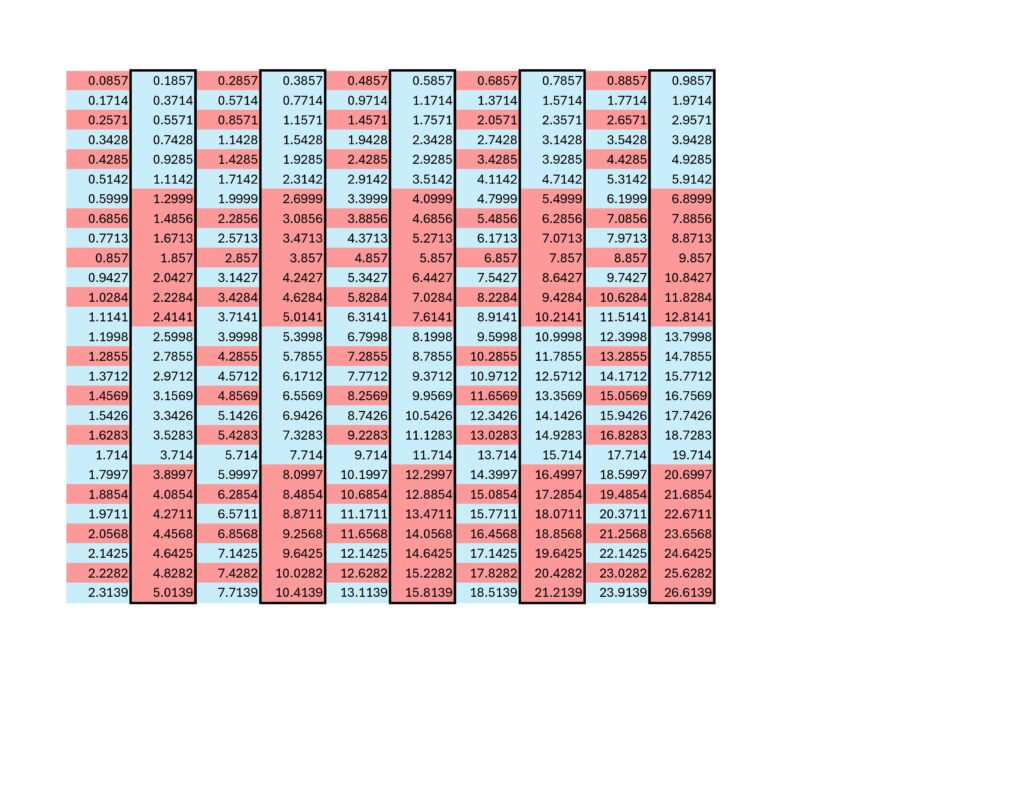
The modulo for the neutron is just as fascinating. It is a very tight, 23-fold symmetry which, to my eye, very slowly counts down toward destruction. Unlike exotics, which decay in a fraction of a nanosecond or faster; a free neutron will decay in around 20 minutes. I’m guessing the modulo provides the countdown to that decay, which if true, corresponds to a neutron spin rate of about 2,000 rotations per second. A non-free neutron, like those found in atomic nuclei, are subjected to constant perturbation; constantly resetting that very long clock and causing those neutrons to remain stable.
Again, if you’re curious, the neutron g-factor is -3.82608545 (you can ignore the negative sign and the integer value, just the remainder is relevant.) 23-fold symmetry has a repeating, 22-digit remainder in between integer values. For 19 divided by 23, the remainder begins with .826 (8260869565217391304347 in full.) Other prime numbers, including 7, 17, 19, 29, 31, 61 and 431 follow the same pattern of their remainders including a repeating set of digits in quantity equal to the prime integer value minus one. In other words, any fraction of 7 will repeat the same 6 numbers, a fraction of 17 will repeat the same 16 numbers, a fraction of 19 will repeat the same 18 numbers, etc.
I know it seems a bit off-topic, but I find the behavior of the above-listed prime numbers fascinating. They are in a set of prime numbers with unique characteristics. Let’s call it the “Coded Prime Set” (because there is a distinct string of numbers, a code, associated with each number in the Set.)
For example, the 7-fold symmetry that drives proton spin, as described above, has its source in the remainder behavior of the prime number 7. Any remainder that follows the sequence 1-4-2-8-5-7, when added to itself will exhibit 7-fold symmetry. Not all prime numbers behave this way; 3, 11 and 13 are not a part of the Set, and neither are other 2-digit primes like 73 and 89. Depending on how you define the Set, there could be an unbounded number of primes that meet the definition of the Set. I have defined the Set more narrowly, so there are a finite number of primes in the Set. That said, the prime number 431 is in the Set and (along with 3 other primes in the Set) is closely associated with the g-factors of the electron and positron.
The sequence has a direction (i.e., it only goes forward, never backward) but is otherwise unrestricted insofar as the sequence can begin with any digit in the sequence, which is determined by which fraction of the prime you are looking at. In the case of the orientation relevant to protons, the sequence begins with 8, so 8-5-7-1-4-2 (which corresponds to 6 divided by 7.) The .X857142 subgroup is where you find the 5.5856946893(16) proton g-factor. That shows the proton owes it’s secondary, 7-fold symmetry (its primary symmetry period is 70,) and consequently some its spinor properties, to the unique behavior of the Coded Prime Set, or more specifically its nested subset, the Mechanical Prime Set.
Incidentally, only the 8-5-7-1-4-2 sequence has a descending 2nd-digit mod order (again, beginning with 9, 8, 7, 5, 4, 2, 1,) while only the 1-4-2-8-5-7 sequence has an ascending 2nd-digit mod order (beginning with 1, 2, 3, 5, 7, 8, 9.) Without either an ascending or descending order, even/odd symmetry cannot be maintained and spinor behavior is not possible. This suggests that the .X142857 subgroup is a strong candidate for the anti-proton g-factor. If that’s the case, I can predict the anti-proton g-factor to be -5.4143053107. Not surprisingly, when you add that remainder to the remainder for the proton g-factor, you get a zero remainder (assuming, of course, you ignore the negative sign like you should.) That was probably an easier way to go about it, but this way was more interesting because it helps to show that the behaviors described are limited to a relatively small subset of the already small Coded Prime Set. Also, I like how this kind of math is non-linear and tends to curve and branch out a bunch. It reminds me of the Mandelbrot Set. Here is an image that may help to give a vague idea of what I am talking about:
In fact, each of the three stable particles which comprise our observable universe, the electron, the proton and the neutron, as well as the 2 additional stable particles (positron and anti-proton) that comprise the unobservable universe (here, “observable” is meant in the astronomical sense,) owe their unique behaviors to their relationship with a specific prime number in the Coded Prime Set, or in the case of the electron and positron; 4 different numbers in the Set (2, 23, 31 and 431.)
First, there is the electron and positron. They are known spinors with a period of 2. I had nothing to do with that particular breakthrough, I just read about it. Then there are the proton and anti-proton which get their spinor behavior from the prime number 7. Next, there is the neutron which gets its stability as well as it’s free decay clock from the prime number 23.
Finally, the electron and positron also appear to additionally relate to both 23 and 31 as well as 431. The 7th-10th digits of the electron g-factor is 3-0-4-3, while the 7th through 10th digits for the positron is 6-9-5-6. I suspect this has something to do with nuclear physics. The 4th-7th digits of the electron and positron g-factors seem to relate somewhat more weakly to 31-fold symmetry, with 4-8-0-6 and 3-1-9-3, respectively. I do not currently have any ideas on what that is all about, in part because the patterns overlap on the 7th digit.
Electrons and positrons share their strongest correlation with the prime number 431, which is in the Coded Prime Set and is also the exact length of the electron/positron integer increment period. The 431 code includes both 0-0-2-3-2-0 and 9-9-7-6-7-9 whereas the electron g-factor remainder begins 0-0-2-3-1-9 and the positron g-factor remainder beings 9-9-7-6-8-0.
I’ll do my best not to make mistakes, but there’s an average chance. Eitherwise, here are the codes in Coded Prime Set (I am not including 43 or 47, or anything over 97… I think the point gets sufficiently made):
2 (1-digit): 5 (electron/positron)
7 (6-digit): 1, 4, 2, 8, 5, 7 (proton/anti-proton)
17 (16-digit): 0, 5, 8, 8, 2, 3, 5, 2, 9, 4, 1, 1, 7, 6, 4, 7
19 (18-digit): 0, 5, 2, 6, 3, 1, 5, 7, 8, 9, 4, 7, 3, 6, 8, 4, 2, 1
23: (22-digit): 0, 4, 3, 4, 7, 8, 2, 6, 0, 8, 6, 9, 5, 6, 5, 2, 1, 7, 3, 9, 1, 3 (neutron, electron/positron)
29 (28-digit): 0, 3, 4, 4, 8, 2, 7, 5, 8, 6, 2, 0, 6, 8, 9, 6, 5, 5, 1, 7, 2, 4, 1, 3, 7, 9, 3, 1
31 (2x 15-digit): 0, 3, 2, 2, 5, 8, 0, 6, 4, 5, 1, 6, 1, 2, 9 – 0, 9, 6, 7, 7, 4, 1, 9, 3, 5, 4, 8, 3, 8, 7 (electron/positron)
61 (60-digit): 0, 1, 6, 3, 9, 3, 4, 4, 2, 6, 2, 2, 9, 5, 0, 8, 1, 9, 6, 7, 2, 1, 3, 1, 1, 4, 7, 5, 5, 4, 9, 8, 3, 6, 0, 6, 5, 5, 7, 3, 7, 7, 0, 4, 9, 1, 8, 0, 3, 2, 7, 8, 6, 8, 8, 5, 2, 4, 5, 9
67 (2x 33-digit): 0, 1, 4, 9, 2, 5, 3, 7, 3, 1, 3, 4, 3, 2, 8, 3, 5, 8, 2, 0, 8, 9, 5, 5, 2, 2, 3, 8, 8, 0, 5, 9, 7, – 0, 2, 9, 8, 5, 0, 7, 4, 6, 2, 6, 8, 6, 5, 6, 7, 1, 6, 4, 1, 7, 9, 1, 0, 4, 4, 7, 7, 6, 1, 1, 9, 4
71 (2x 35-digit): 0, 1, 4, 0, 8, 4, 5, 0, 7, 0, 4, 2, 2, 5, 3, 5, 2, 1, 1, 2, 6, 7, 6, 0, 5, 6, 3, 3, 8, 0, 2, 8, 1, 6, 9 – 0, 9, 8, 5, 9, 1, 5, 4, 9, 2, 9, 5, 7, 7, 4, 6, 4, 7, 8, 8, 7, 3, 2, 3, 9, 4, 3, 6, 6, 1, 9, 7, 1, 8, 3
83 (2x 41-digit): 0, 1, 2, 0, 4, 8, 1, 9, 2, 7, 7, 1, 0, 8, 4, 3, 3, 7, 3, 4, 9, 3, 9, 7, 5, 9, 0, 3, 6, 1, 4, 4, 5, 7, 8, 3, 1, 3, 2, 5, 3 – 0, 2, 4, 0, 9, 6, 3, 8, 5, 5, 4, 2, 1, 6, 8, 6, 7, 4, 6, 9, 8, 7, 9, 5, 1, 8, 0, 7, 2, 2, 8, 9, 1, 5, 6, 6, 2, 6, 5, 0, 6
97 (96-digit): 0, 1, 0, 3, 0, 9, 2, 7, 8, 3, 5, 0, 5, 1, 5, 4, 6, 3, 9, 1, 7, 5, 2, 5, 7, 7, 3, 1, 9, 5, 8, 7, 6, 2, 8, 8, 6, 5, 9, 7, 9, 3, 8, 1, 4, 4, 3, 2, 9, 8, 9, 6, 9, 0, 7, 2,1, 6, 4, 9, 4, 8, 4, 5, 3, 6, 0, 8, 2, 4, 7, 4, 2, 2, 6, 8, 0, 4, 1, 2, 3, 7, 1, 1, 3, 4, 0, 2, 0, 6,1, 8, 5, 5, 6, 7
What you are looking at are fixed paths, mathematically carved into the foundation of reality, and not merely the result of arbitrary and abstract equations (i.e., most integers you can take apart any which way, and put them back together similarly, but these numbers have only one way to be taken apart and one way to be put back together… except in the case of Type-B coded primes like 31 and 431 where there are technically 2 ways.) It is not coincidence that the calculated g-factors for protons, neutrons and electrons (and thereby positrons and anti-protons (as well as twotrons)) in other words all known, stable particles, track so closely. There is a lot to unpack, but in short, a string of at least 3+ digits (i.e., a bit more than 3, not quite 4) is needed for a minimal, recognizable relation to a code, with more digits bringing you closer (these are infinitely repeating strings, so you never quite get there.) Also, these values are interrelated, internally logarithmic and all a bit wibbly-wobbly, timey-wimey. For more info, see the post for The Mechanical Prime Set. A map is desperately needed. I guess it wasn’t so off-topic after all. More to come later.
Since you made it to the bottom of the page, here is an unhinged rant on a common refrain I hear from people with clinically low levels of imagination… click here!