I was recently challenged with the idea that the neutron should have an anti-particle. Mathematically, it should, and so I’ve decided it does. I’m calling it the twotron. Best guess is that neutrons decay into protons and electrons while twotrons decay into anti-protons and positrons. More importantly, the evidence shows that five specific prime numbers have a direct influence on physical reality.
**5.13.24 update** The scope of this page has expanded to include the electron and positron as well as prime numbers 31 and 431.
**5.18.24 update** The page has been refocused to demonstrating and describing the Mechanical Prime Set, which includes 2, 7, 23, 31 and 431.
**5.27.24 update** The page has been updated to include a set definition at the top.
C. Brian Conkle
[last updated 5.27.24] May 10, 2024
Vancouver, WA
contact@triforce.fyi
* added 5.27.24:
Mechanical Prime Set Definition:
Any prime number within the Coded Prime Set with a distribution of fractional values such that in an additive modular (“modulo”) mathematics analysis x+n=y; where x = the first remainder digit, y = the number which precedes x on the fractional value “code” for the prime number, n = a rotational offset value with integral values between 0 and 9, and where values for n are normally distributed, with at least one pair of fractional values demonstrating ascending followed by descending order in between zero-remainder rotations.
There are five known prime numbers which meet this definition: 2, 7, 23, 31 and 431. These are also the same 5 prime numbers which have a direct correlation to the calculated g-factors for electrons, protons, neutrons and their anti-particles.
The combination of all of the above is where the Mechanical Prime Set gets its name.
* start of original post:
I couldn’t help but try and figure out exactly how the neutron, twotron, electron and positron were related to the number 23. My suspicion is that the number provides the rotation instructions for the neutron and twotron, while I have no idea how the electron and positron are involved. I know how it sounds to say the number 23 contains all the instructions needed for neutrons and twotrons to spin… nothing I can do about that. I didn’t create reality, I’m just describing it.
OK, it takes a bit more than just the number 23 to teach a neutron how to spin. Specifically, 4 pieces of information are required.
First, you need the quotient remainder code. This comes from the fractions of 23 and looks like this: 0, 4, 3, 4, 7, 8, 2, 6, 0, 8, 6, 9, 5, 6, 5, 2, 1, 7, 3, 9, 1, 3
Second, if you consider every -3.826086 and 3.173913 revolutions to be 1 “spin,” then you need to know your spin number (i.e., what fraction of 23 are you on?) Neutron spin is counter clockwise while twotron spin is clockwise.
Third, you need to know the static pattern 1, 1, 1, 2, 2, 3, 3, 4, 4, 4, 4, 6, 6, 6, 6, 7, 7, 8, 8, 9, 9, 9 (possibly, 1, 1, 1, 2, 2, 3, 3, 4, 4, 4, 4, -4, -4, -4, -4, -3, -3, -2, -2, -1, -1, -1) This comes from the fractions 4/23 and 19/23 specifically. Other fractions of 23 have essentially arbitrary patterns. The pattern is just a simple, mechanical spacing operation; incrementally rotating between one to four degrees of separation, in ascending order for the first half of the cycle following a zero remainder, and in descending order for the cycle’s back half.
Fourth and finally, you need to know the first digit of the quotient remainder. If you think of it as standing on a clock with 10 hours, numbered 0-9; this means you know which hour you are standing on.
With those 4 pieces of information, the exact rotational path of the neutron and twotron can be predicted to a level of granularity commensurate with proximity to the precise quotient remainder code for 23. Put another way, those four bits of information are all you need to generate 23-fold rotational symmetry.
I know this is pretty high concept, so here is a visual aid:
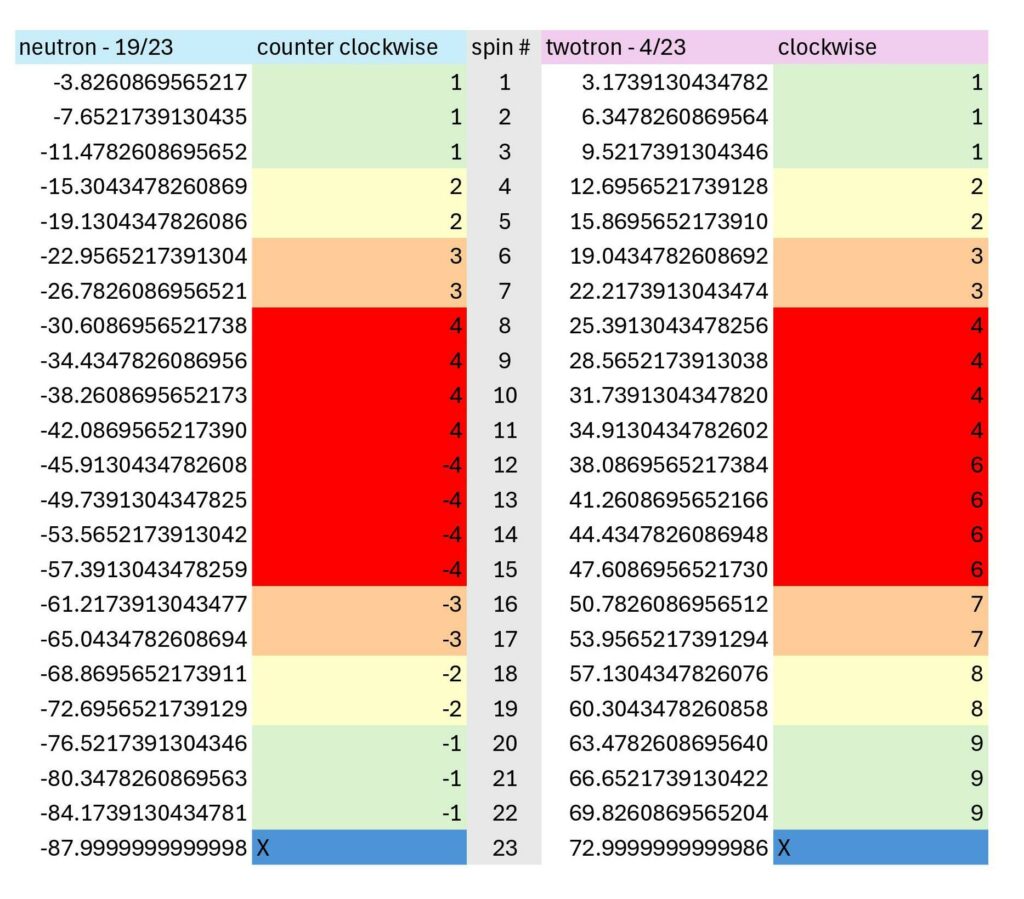
The main issue is that the quotient remainder for 23 has 22 digits, which means all numbers from 0-9 are included twice while 3 and 6 are included 3 times. So, if you are on, for example, a 6; how do you know which 6 you are on? The static value chart (the color-coded part of the spreadsheet) gives the answer. The above spreadsheet combines all the required information, including the quotient remainder code, but here is that again for easy reference: 0, 4, 3, 4, 7, 8, 2, 6, 0, 8, 6, 9, 5, 6, 5, 2, 1, 7, 3, 9, 1, 3.
The easiest way to understand this is by looking at the first few spins of the twotron. For the first 3 spins, a value of 1 is indicated on the static chart. This means the number preceding the first remainder digit will be 1 number higher than the first remainder digit. This is an unseen digit.
Here is the same spreadsheet, but this one has only the required information and is in puzzle form:
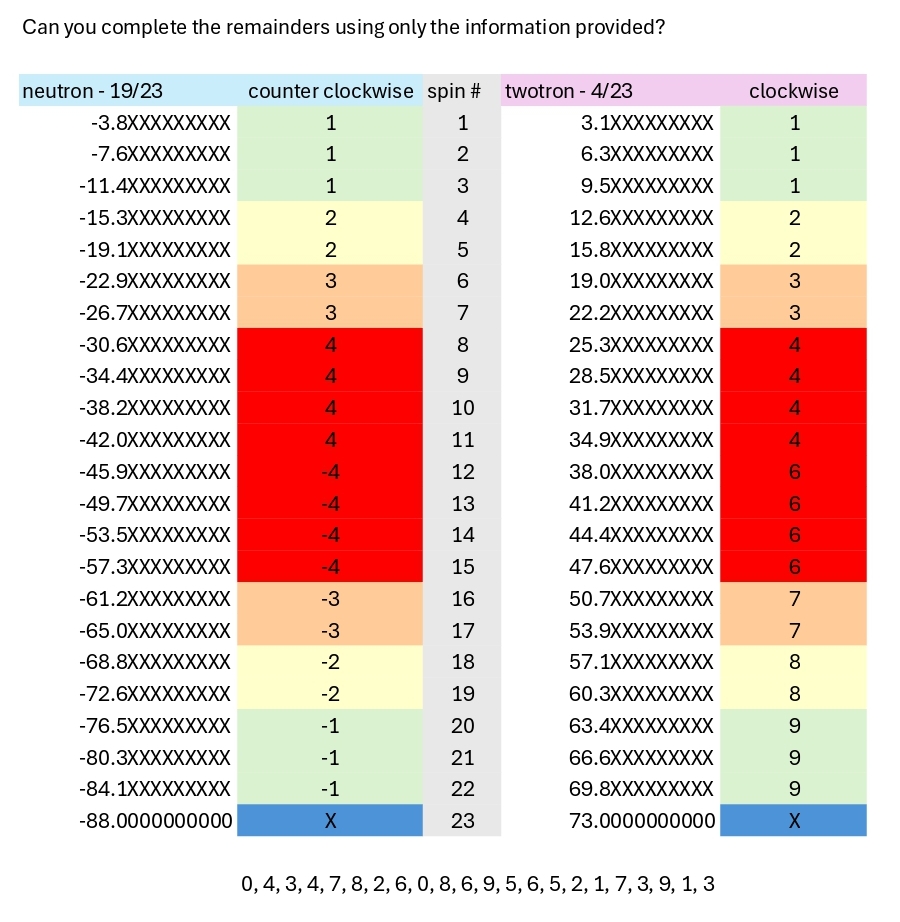
On spin 1, the first remainder digit is 1, so the preceding (unseen) number is 2. That means the remainder goes 1, 7, 3, 9 rather than 1, 3, 0, 4.
On spin 2, the first remainder digit is 3, so the preceding (unseen) number is 4. That means the remainder goes 3, 4, 7, 8 rather than 3, 0, 4, 3 or 3, 9, 1, 3.
On spin 3, the first remainder digit is 5, so the preceding (unseen) number is 6. That means the remainder goes 5, 2, 1, 7 rather than 5, 6, 5, 2.
On spin 4, the first remainder digit is 6, so the preceding (unseen) number is 8. That means the remainder goes 6, 9, 5, 6 rather than 6, 0, 8, 6 or 6, 5, 2, 1.
And so on and so forth.
So, if all a neutron or twotron needs to spin is those 4 bits of information, the question is then how does it store and read that information? How does the particle know at what decimal fraction of rotation it is on or how many times it has spun since its last zero-remainder spin? I don’t have the answers just yet, but I know the above detail is the key.
I found the same type of modular behavior in the prime 31; no surprise, by looking exactly where the electron g-factor told me to look (specifically, where the 4th-7th remainder digits of the electron and positron g-factors line up most closely with the 2nd-5th digits of a fraction of 23. That corresponds to 8/31 and 23/31.) Here is both a filled-in chart and a chart in puzzle form. I am not including the spin # because that would require reorienting to landscape and I decline… counting is still an option if you like.
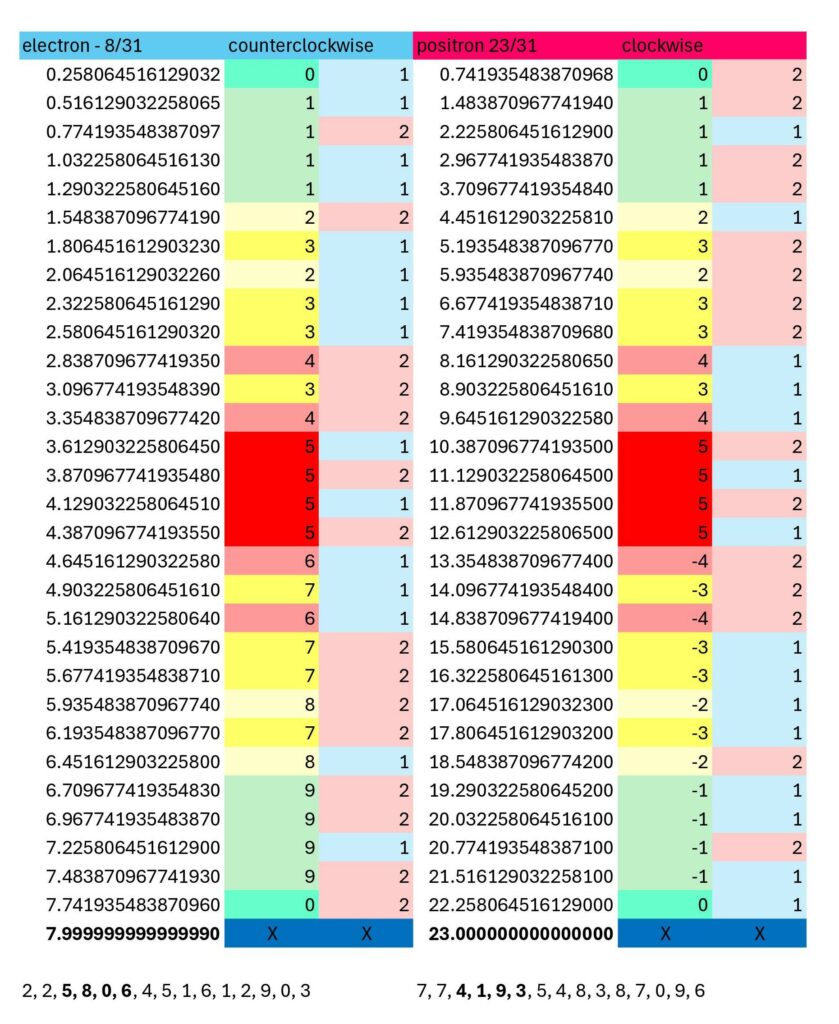
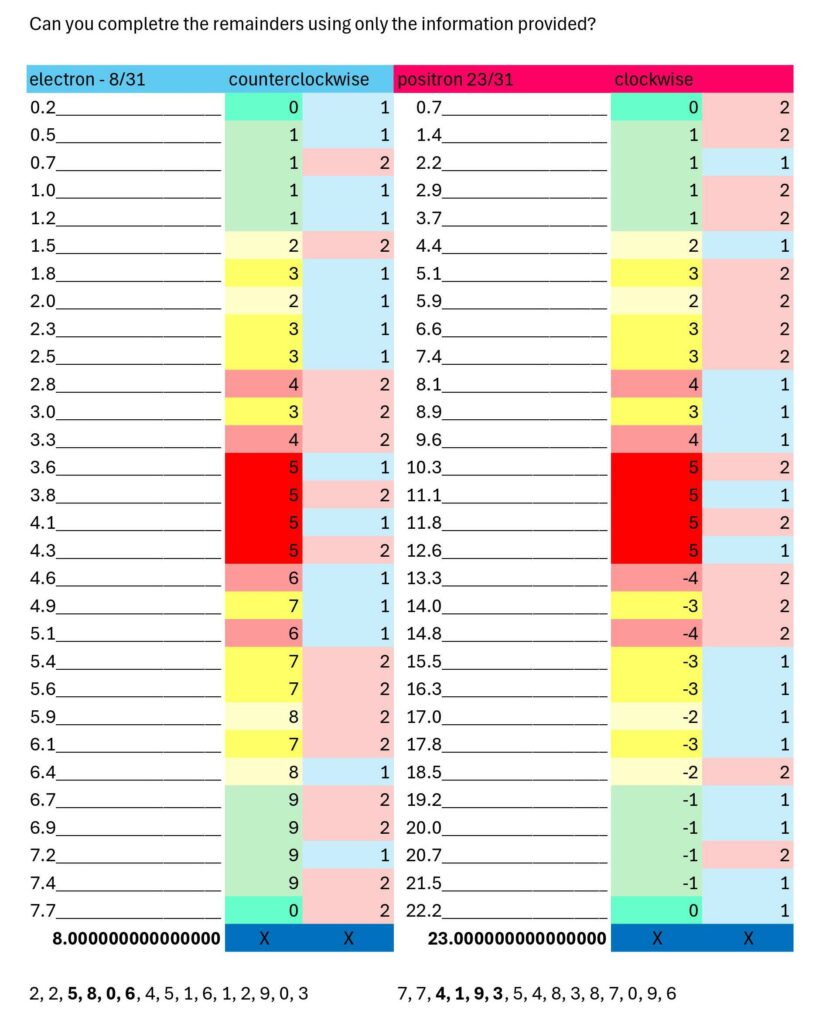
I suspect this same modular behavior exists in the prime 431 as well. I’m curious if they are the only primes that do this (17, 19 and 29 do not,) or if there are others. (Since you read this far, here is a clue for the electron puzzle… the 2nd column that is color-coded red and blue is a red herring; it does not have any impact on the determination of the remainder… but it does seem to suggest something I do not know what.)
I couldn’t help myself and I looked at 431 as well. It is pretty much exactly what I expected. The electron and positron correlate directly to 1/431 and 430/431, but with a code this size, a single digit is not sufficient to ascertain location on the string. A second digit is needed, so the rotational symmetry normalizes on 10/431 for the electron rather than 1/431. This corresponds to 421/431 for the positron which behaves as expected.
I don’t see any other prime numbers behaving this way, even within the Coded Prime Set; showing this level of modular fidelity as well as modular symmetry. I feel confident stating the prime numbers 2, 7, 23, 31 and 431 are nested set within the Coded Prime Set.
I originally named this nested set the “Modular Prime Set” (“modular” meaning math on a circle as opposed to math on a line,) and suggested the “G-Factor Set” would also be appropriate because only the prime numbers 2, 7, 23, 31 and 431 were represented in g-factor values, while only those prime numbers appear to have symmetrical, modular behavior.
That being said, I am now of a mind that the optimal name to give it is the “Mechanical Prime Set.” The deeper context for the unique modular symmetry of this Set, and its correlation to subatomic particle g-factors, is that these, and only these, prime numbers have internal structures which are mechanically stable (i.e., if you were so inclined, you could replicate these characteristics will normal, mostly symmetrical bits of clockwork.)
In the case of primes 2 and 7, mechanical stability comes from simplicity; a single, repeating digit (5) or the same six, repeating digits (1-4-2-8-5-7,) respectively.
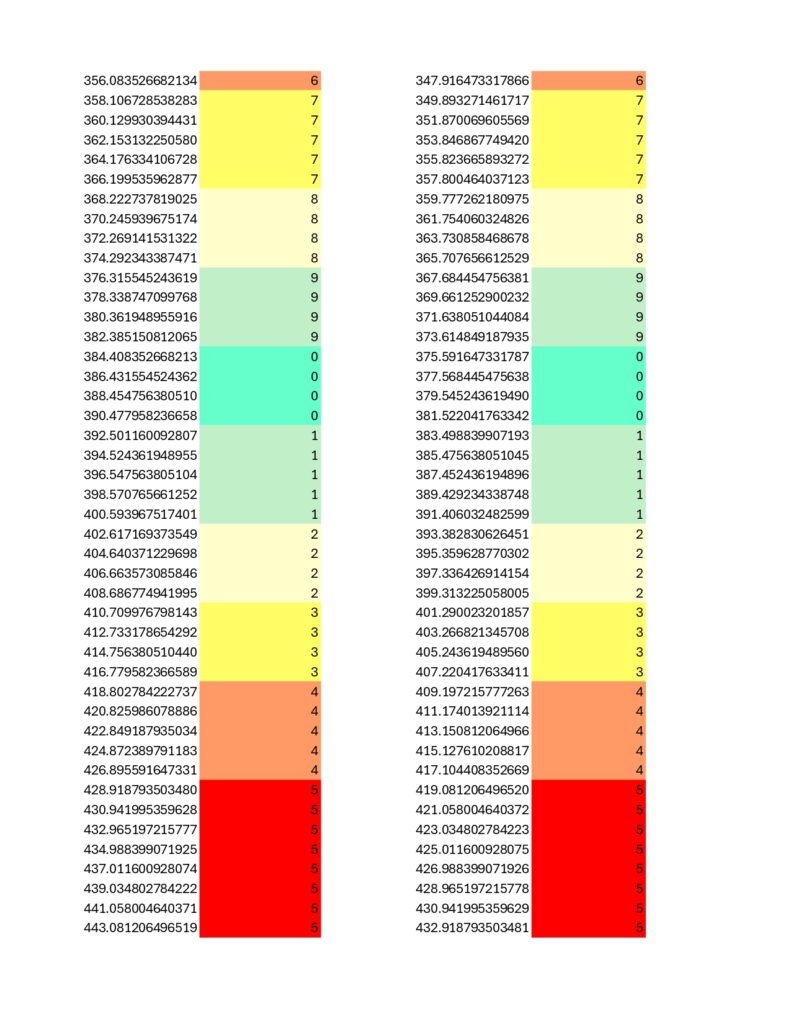
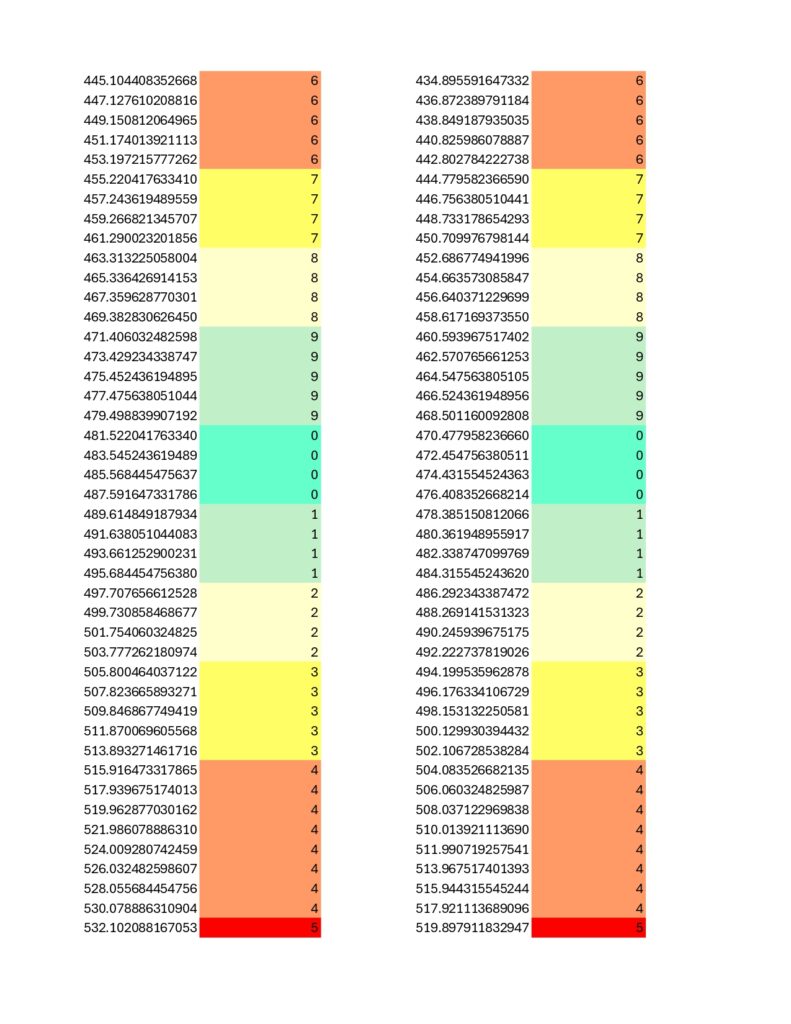
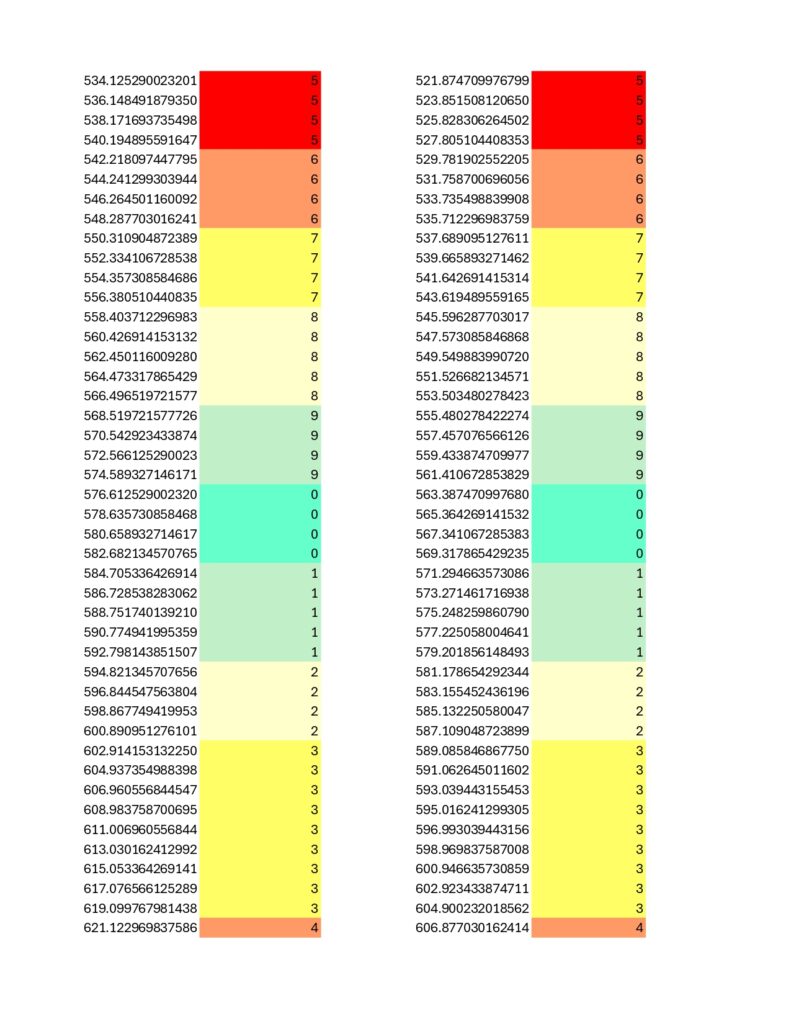
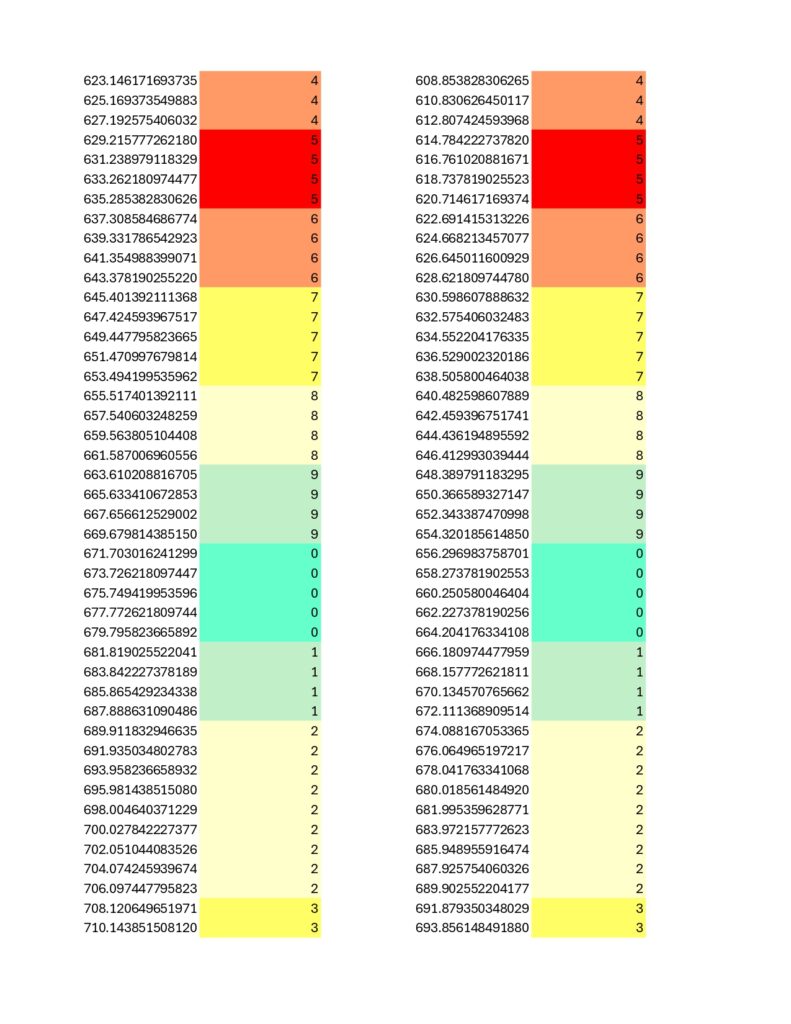
For prime numbers 23, 31, and 431, mechanical stability arises from increasingly complex internal structure. To some extent, all prime numbers in the Coded Prime Set exhibit this type of modular behavior, but only in the cases of 23 and 431 is that modular behavior roughly symmetrical and therefore not inherently arbitrary.
The prime 31 is more of a near miss as the immediately above spreadsheets show a bit of a wobble not present in primes 23 and 431. Eitherwise, and speaking of; here is the chart for 431… it is about as filled in as the 2nd Death Star was at the time of the Battle of Endor. No puzzle for this one, but do notice the high degree of internal symmetry, on par with the results for prime number 23 while exceeding that of 31:
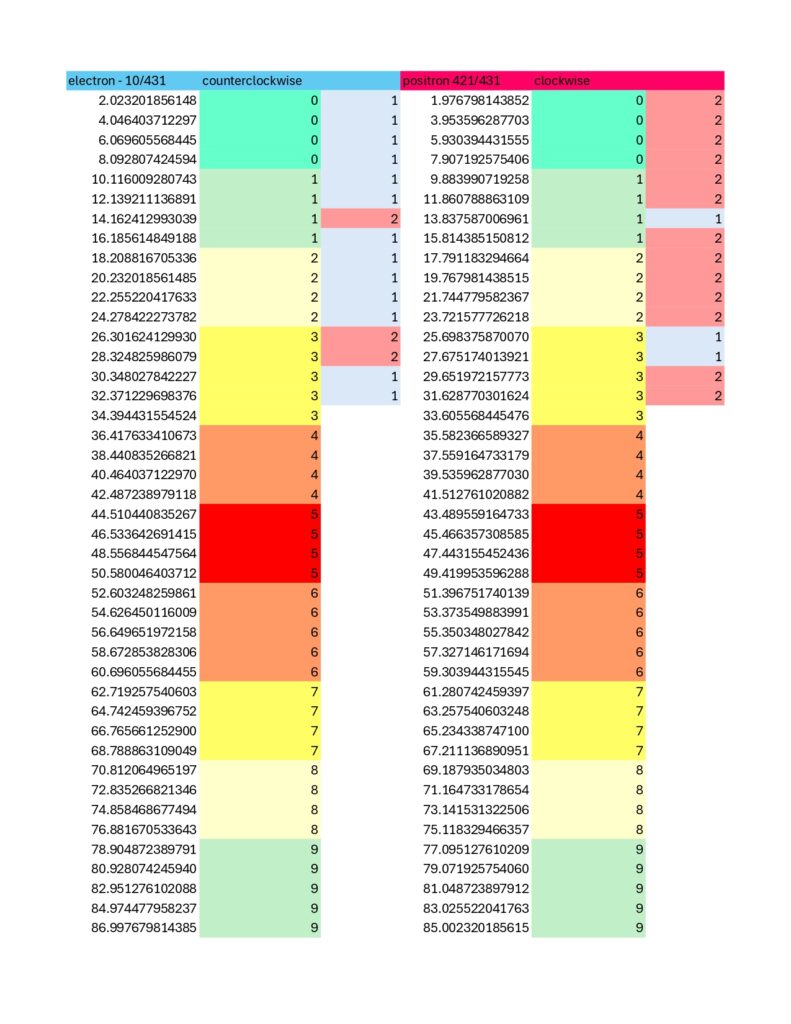
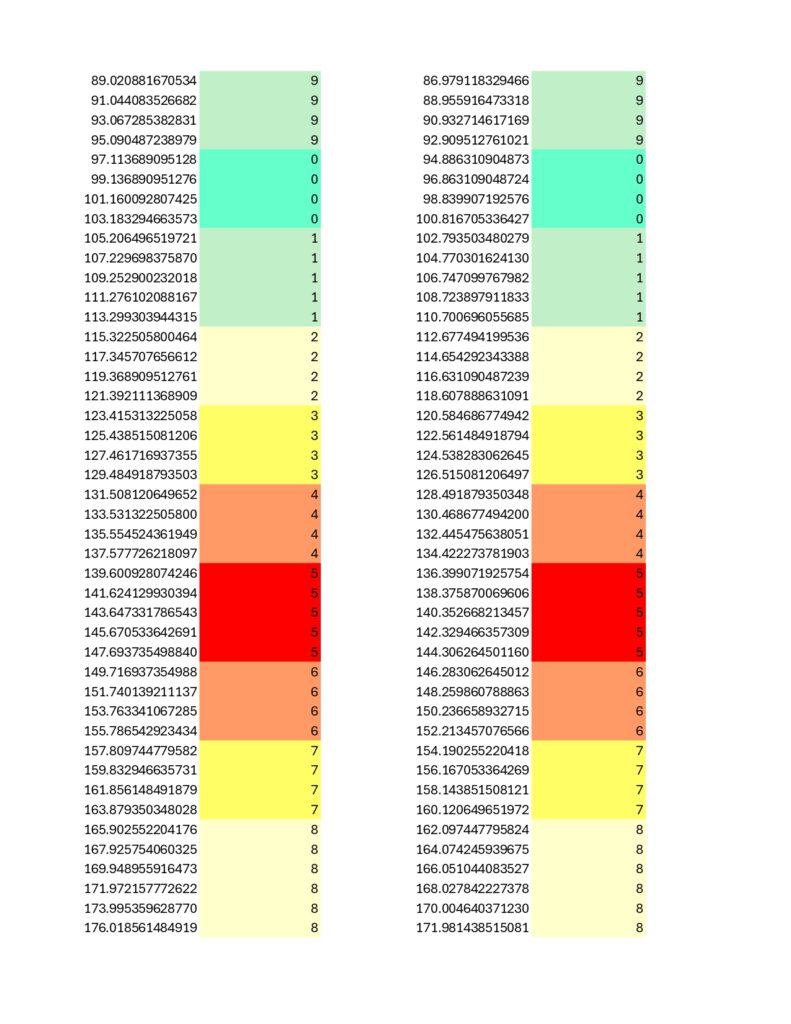
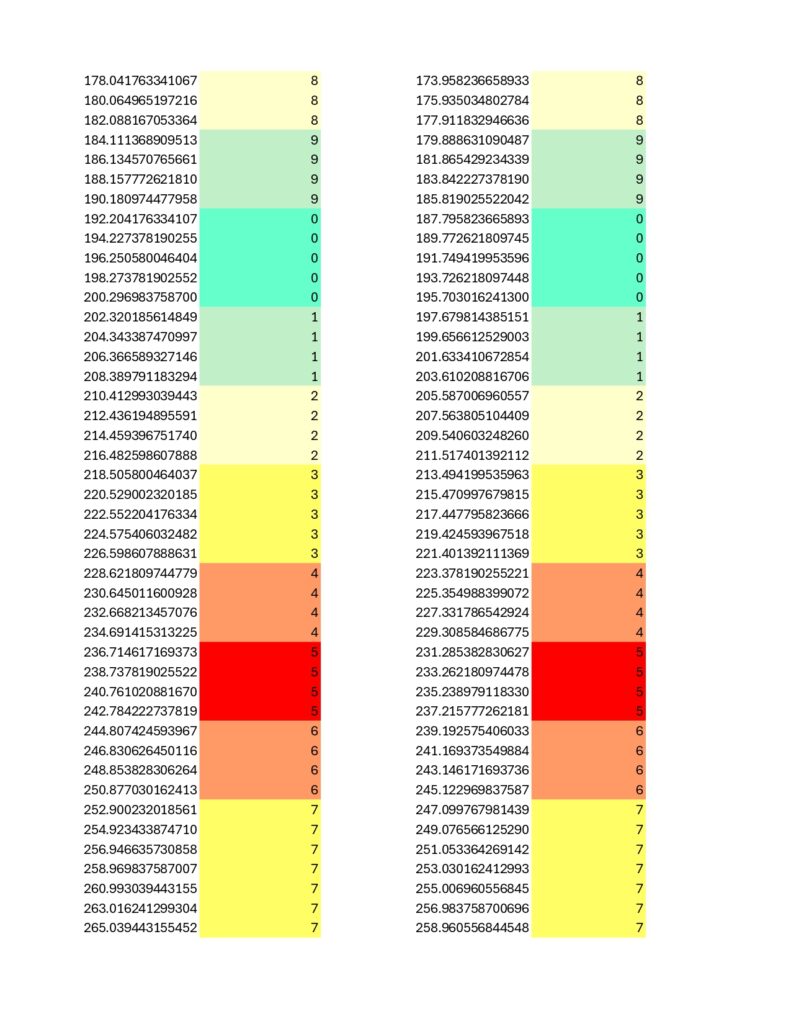
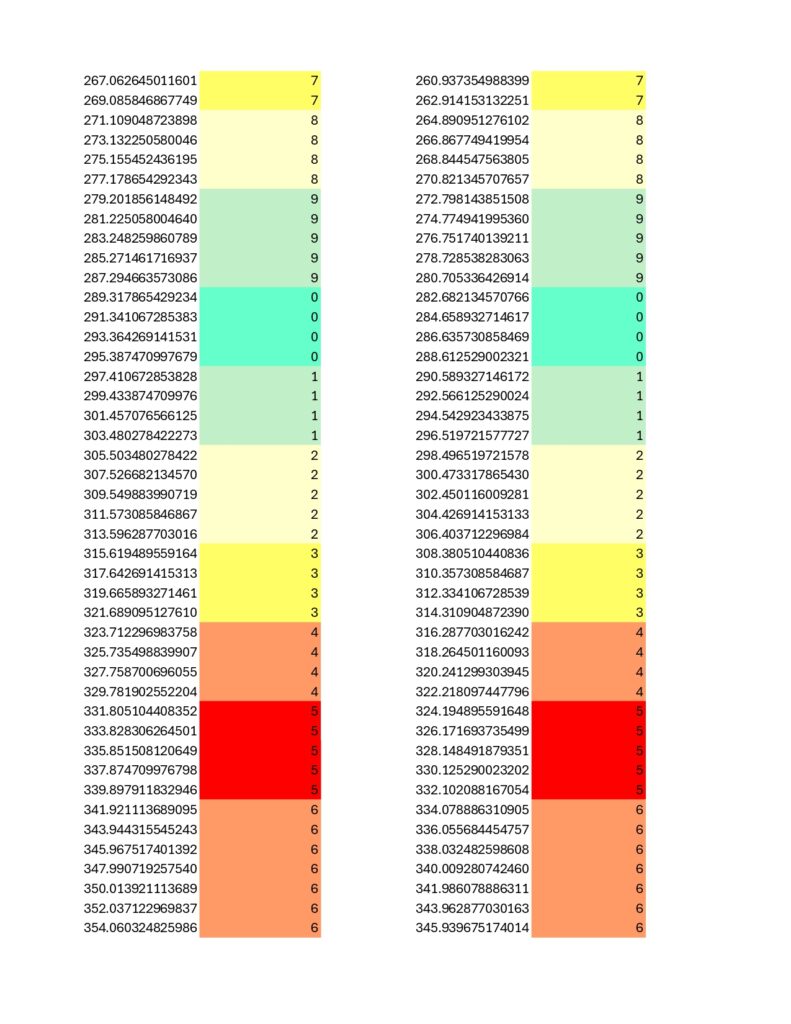
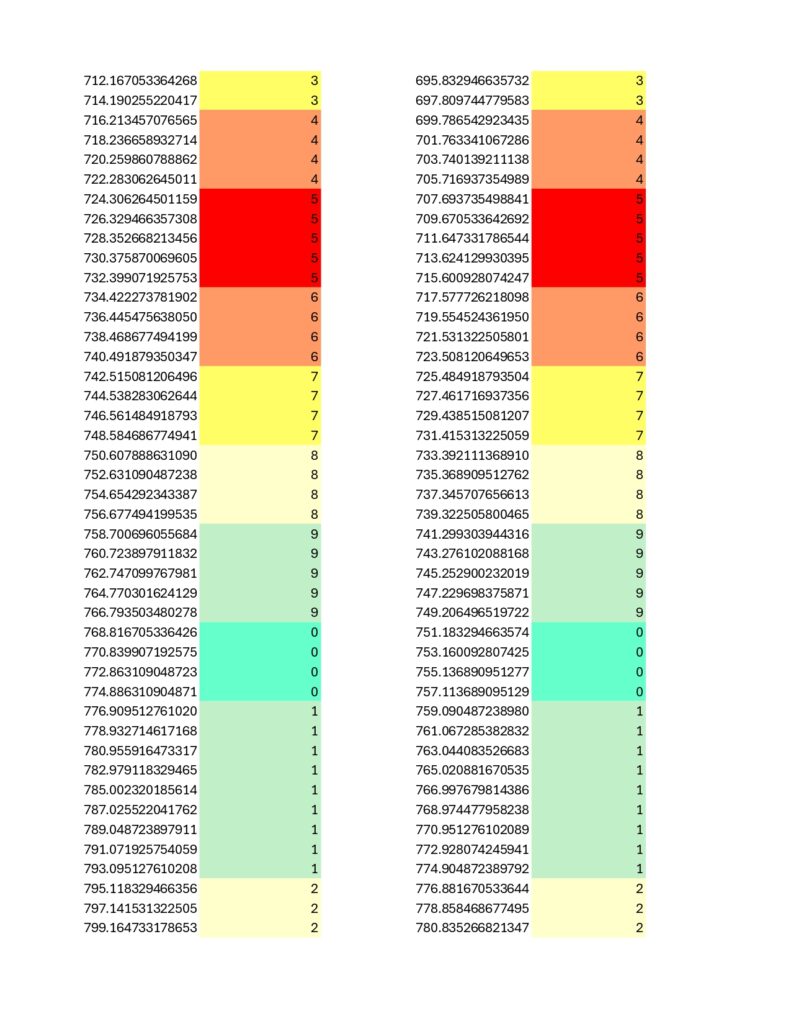

More to come later.