There is a very clear, close connection between subatomic particle spin, anomalous magnetic moment and the coded fractional values of this Set of prime numbers
C. Brian Conkle
May 7, 2024
Vancouver, WA
contact@triforce.fyi
Coded Prime Set Definition:
Any prime number with fractional values containing a non-repeating, infinitely looped string of digits with string length = p-1, where “p” is the prime number, is a part of the Set and is a “Type-A” coded prime number. Any prime number with fractional values containing a pair of infinitely repeating, looped strings of digits with string length =(p-1)÷2, where “p” is the prime number, is a part of the Set and is a “Type-B” coded prime number. All other numbers are not in the Set.
Type-A Examples:
Fractions of the prime number 7 are comprised of the following repeating string of 6 digits: 1, 4, 2, 8, 5, 7
Fractions of the prime number 17 are comprised of the following repeating string of 16 digits: 0, 5, 8, 8, 2, 3, 5, 2, 9, 4, 1, 1, 7, 6, 4, 7.
Fractions of the prime number 23 are comprised of the following repeating string of 22 digits: 0, 4, 3, 4, 7, 8, 2, 6, 0, 8, 6, 9, 5, 6, 5, 2, 1, 7, 3, 9, 1, 3.
Type-B Examples:
Fractions of the prime number 31 are comprised of the two following repeating strings of 15 digits: 0, 3, 2, 2, 5, 8, 0, 6, 4, 5, 1, 6, 1, 2, 9 – 0, 9, 6, 7, 7, 4, 1, 9, 3, 5, 4, 8, 3, 8, 7
Fractions of the prime number 67 are comprised of the two following repeating strings of 33 digits: 0, 1, 4, 9, 2, 5, 3, 7, 3, 1, 3, 4, 3, 2, 8, 3, 5, 8, 2, 0, 8, 9, 5, 5, 2, 2, 3, 8, 8, 0, 5, 9, 7, – 0, 2, 9, 8, 5, 0, 7, 4, 6, 2, 6, 8, 6, 5, 6, 7, 1, 6, 4, 1, 7, 9, 1, 0, 4, 4, 7, 7, 6, 1, 1, 9, 4
There are an unbounded number of prime numbers, and the Coded Prime Set is also unbounded. The Mechanical Prime Set, however, may actually be bounded.
While there are prime numbers which could meet the definition of a Type-C coded prime (in fact there could be as many as 10 different types, encompassing all prime numbers,) there are reasons (relating mostly to particle/anti-particle symmetry) why only two types of coded primes, Type-A and Type-B, can be said to meet the definition of a “coded” prime number.
Relationship Between the Coded Prime Set and the Behavior of Subatomic Particles
There are 3 stable subatomic particles, two of which have known anti-particles (analysis suggests the neutron also has an anti-particle, I call it the “twotron.”) So, in total there are 6 stable particles we can observe or intuit: (1) electron, (2) positron, (3) proton, (4) anti-proton, (5) neutron and (6) twotron. The electron, proton and neutron all have measured values for something called its g-factor. It is essentially a composite value describing a particle’s anomalous magnetic moment, momentum, spin and mass. If you have any further questions about the g-factor, I refer you to the interwebs. Suffice it to say, I did not calculate any g-factor values myself other than for the positron, anti-proton and twotron, and I only calculated those values because nobody ever has before.
The way the g-factor operates is to provide a two-dimensional, rotational offset value, based on anomalous magnetic moment that determines, essentially, at what point along a particle’s rotational path its magnetic moment expresses. In other words, it operates in pretty much the same way as Wheel of Fortune or spin the bottle. Because particles have an internal frame of reference, the particle “knows” when it has completed one rotation and begun another. Actually, it’s more than that, the particle doesn’t just know where it is along its rotational path; it is continually told/updated where it is along its rotational path by the coded nature of the prime number-generated symmetry which constitutes its rotational path. Eitherwise, the g-factor determines how far along in its rotational path the torque of magnetic moment will be applied.
Calculated g-factors for all stable subatomic particles are extremely closely correlated to the Coded Prime Set
It is interesting how closely correlated the calculated g-factors for the electron (and thereby the positron,) proton (and thereby the anti-proton,) and the neutron are to the Coded Prime Set. The proton/anti-proton has a single, 5-digit correlation to prime number 7. The neutron g-factor has a single, 6-digit correlation to prime number 23. Finally, the electron/positron has four distinct correlations to prime numbers, 2 (1-digit correlation) 23 (4-digit correlation) 31 (4-digit correlation) and 431 (6-digit correlation.)
Reproduced from Page 1 of the site, here is the detail on Coded Prime Set, this time with some additional detail for prime 431:
2 (1-digit): 5 (electron/positron)
7 (6-digit): 1, 4, 2, 8, 5, 7 (proton/anti-proton)
17 (16-digit): 0, 5, 8, 8, 2, 3, 5, 2, 9, 4, 1, 1, 7, 6, 4, 7
19 (18-digit): 0, 5, 2, 6, 3, 1, 5, 7, 8, 9, 4, 7, 3, 6, 8, 4, 2, 1
23: (22-digit): 0, 4, 3, 4, 7, 8, 2, 6, 0, 8, 6, 9, 5, 6, 5, 2, 1, 7, 3, 9, 1, 3 (neutron/twotron, electron/positron)
29 (28-digit): 0, 3, 4, 4, 8, 2, 7, 5, 8, 6, 2, 0, 6, 8, 9, 6, 5, 5, 1, 7, 2, 4, 1, 3, 7, 9, 3, 1
31 (2x 15-digit): 0, 3, 2, 2, 5, 8, 0, 6, 4, 5, 1, 6, 1, 2, 9 – 0, 9, 6, 7, 7, 4, 1, 9, 3, 5, 4, 8, 3, 8, 7 (electron/positron)
431 (2x 215-digit): 0, 0, 2, 3, 2, 0, 1, 8, 5, 6, 1, 4, 8, 4, 9, 1, 8, 7, 9, 3, 5, 0, 3, 4, 8, 0, 2, 7, 8, 4, 2, 2, 2, 7, 3, 7, 8, 1, 9, 0, 2, 5, 5, 2, 2, 0, 4, 1, 7, 6, 3, 3, 4, 1, 0, 6, 7, 2, 8, 5, 3, 8, 2, 8, 3, 0, 6, 2, 6, 4, 5, 0, 1, 1, 6, 0, 0, 9, 2, 8, 0, 7, 4, 2, 4, 5, 9, 3, 9, 6, 7, 5, 1, 7, 4, 0, 1, 3, 9, 2, 1, 1, 1, 3, 6, 8, 9, 0, 9, 5, 1, 2, 7, 6, 1, 0, 2, 0, 8, 8, 1, 6, 7, 0, 5, 3, 3, 6, 4, 2, 6, 9, 1, 4, 1, 5, 3, 1, 3, 2, 2, 5, 0, 5, 8, 0, 0, 4, 6, 4, 0, 3, 7, 1, 2, 2, 9, 6, 9, 8, 3, 7, 5, 8, 7, 0, 0, 6, 9, 6, 0, 5, 5, 6, 8, 4, 4, 5, 4, 7, 5, 6, 3, 8, 0, 5, 1, 0, 4, 4, 0, 8, 3, 5, 2, 6, 6, 8, 2, 1, 3, 4, 5, 7, 0, 7, 6, 5, 6, 6, 1, 2, 5, 2, 9 – 0, 0 (incomplete) … 8, 7, 4, 7, 0, 9, 9, 7, 6, 7, 9, 8, 1, 4, 3, 8, 5, 1, 5… (electron/positron)
43 (2x 21-digit): 0, 2, 3, 2, 5, 5, 8, 1, 3, 9, 5, 3, 4, 8, 8, 3, 7, 2, 0, 9, 3 – 0, 4, 6, 5, 1, 1, 6, 2, 7, 9, 0, 6, 9, 7, 6, 7, 4, 4, 1, 8, 6
47 (46-digit): 0, 2, 1, 2, 7, 6, 5, 9, 5, 7, 4, 4, 6, 8, 0, 8, 5, 1, 0, 6, 3, 8, 2, 9, 7, 8, 7, 2, 3, 4, 0, 4, 2, 5, 5, 3, 1, 9, 1, 4, 8, 9, 3, 6, 1, 7
61 (60-digit): 0, 1, 6, 3, 9, 3, 4, 4, 2, 6, 2, 2, 9, 5, 0, 8, 1, 9, 6, 7, 2, 1, 3, 1, 1, 4, 7, 5, 5, 4, 9, 8, 3, 6, 0, 6, 5, 5, 7, 3, 7, 7, 0, 4, 9, 1, 8, 0, 3, 2, 7, 8, 6, 8, 8, 5, 2, 4, 5, 9
67 (2x 33-digit): 0, 1, 4, 9, 2, 5, 3, 7, 3, 1, 3, 4, 3, 2, 8, 3, 5, 8, 2, 0, 8, 9, 5, 5, 2, 2, 3, 8, 8, 0, 5, 9, 7, – 0, 2, 9, 8, 5, 0, 7, 4, 6, 2, 6, 8, 6, 5, 6, 7, 1, 6, 4, 1, 7, 9, 1, 0, 4, 4, 7, 7, 6, 1, 1, 9, 4
71 (2x 35-digit): 0, 1, 4, 0, 8, 4, 5, 0, 7, 0, 4, 2, 2, 5, 3, 5, 2, 1, 1, 2, 6, 7, 6, 0, 5, 6, 3, 3, 8, 0, 2, 8, 1, 6, 9 – 0, 9, 8, 5, 9, 1, 5, 4, 9, 2, 9, 5, 7, 7, 4, 6, 4, 7, 8, 8, 7, 3, 2, 3, 9, 4, 3, 6, 6, 1, 9, 7, 1, 8, 3
83 (2x 41-digit): 0, 1, 2, 0, 4, 8, 1, 9, 2, 7, 7, 1, 0, 8, 4, 3, 3, 7, 3, 4, 9, 3, 9, 7, 5, 9, 0, 3, 6, 1, 4, 4, 5, 7, 8, 3, 1, 3, 2, 5, 3 – 0, 2, 4, 0, 9, 6, 3, 8, 5, 5, 4, 2, 1, 6, 8, 6, 7, 4, 6, 9, 8, 7, 9, 5, 1, 8, 0, 7, 2, 2, 8, 9, 1, 5, 6, 6, 2, 6, 5, 0, 6
97 (96-digit): 0, 1, 0, 3, 0, 9, 2, 7, 8, 3, 5, 0, 5, 1, 5, 4, 6, 3, 9, 1, 7, 5, 2, 5, 7, 7, 3, 1, 9, 5, 8, 7, 6, 2, 8, 8, 6, 5, 9, 7, 9, 3, 8, 1, 4, 4, 3, 2, 9, 8, 9, 6, 9, 0, 7, 2,1, 6, 4, 9, 4, 8, 4, 5, 3, 6, 0, 8, 2, 4, 7, 4, 2, 2, 6, 8, 0, 4, 1, 2, 3, 7, 1, 1, 3, 4, 0, 2, 0, 6,1, 8, 5, 5, 6, 7
For additional context, here is a reproduction of the summary mod analysis from Page 1:
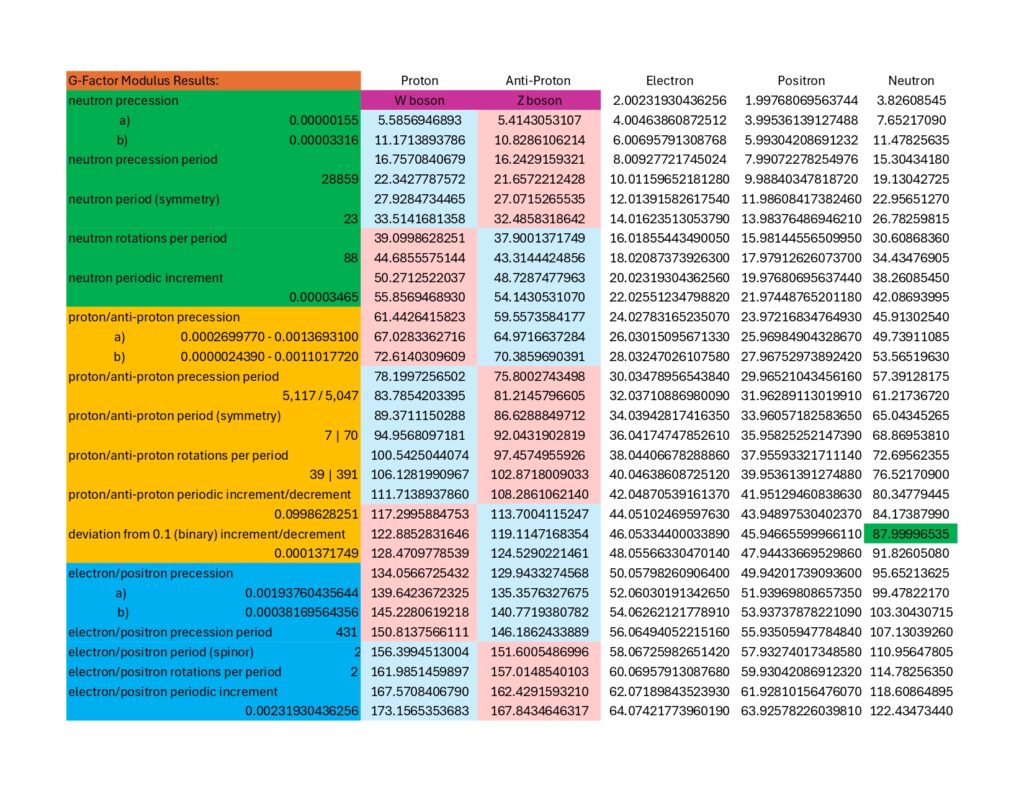
There is a direct link between the fundamental behaviors of subatomic particles and the Coded Prime Set. It warrants further inquiry. Also, commissioning and creation of a map of all spin states is warranted. The next step, however, is defining and describing the Mechanical Prime Set. More to come later.